
Relativně = vzhledem k jinému (tělesu).
Těleso je v klidu či v pohybu vždy vzhledem (relativně)
k jinému tělesu.
Já jsem v klidu (např. vůči Zemi) a zároveň v pohybu (např. vůči Slunci).
Trajektorie = "čára" nakreslená pohybem tělesa (spojnice poloh, kterými prošel bod tělesa).
Dráha = délka trajektorie (vzdálenost uražená tělesem).
- přímočarý (na krátkém úseku letadlo, vlak, řeka…)
trajektorie = přímka
- křivočarý (většina pohybů - zvířata, technika, nářadí…)
trajektorie = křivka
* posuvný (dopr. prostředky, chůze…)
trajektorie = přímka nebo křivka
* otáčivý (kolo, páka…)
"stopa" bodu tělesa = kružnice
osa otáčení = střed těchto kružnic
| podle trajektorie (přímočarý - křivočarý) |
podle
posunu (posuvný - otáčivý) |
|
| auto ve městě | křivočarý | posuvný |
| klika flašinetu obr | křivočarý | otáčivý |
| pád kapky | přímočarý | posuvný |
Kolo auta se zároveň otáčí i posunuje - koná pohyb složený.
Video: trajekt (0:37-2:00), přímoč+křivoč 4:08-4:31), přímoč+křivoč (6:43-13:55), posuvný+otáčivý pohyb (0:52-10:27)
Kviz: skn-posuvny-ot
| uveď 2 příklady: | přímočarý | křivočarý |
| posuvný | letadlo, řeka | had, žák |
| otáčivý | - | kolo, Měsíc |
Uveď příklady těles:
| vzhledem k -> | kolotoč | jedoucí vlak | řidič jedoucího auta |
| se pohybuje: | tráva | koleje | šroub v kole |
| se nepohybuje: | sedátko | dveře WC | airbag |
Charakterizuj pohyb: míč po výkopu z brány, šroubování šroubu, kolo auta za jízdy.
Urči, zda je pohyb rovnoměrný či nerovnoměrný + kdo se takovým pohybem může pohybovat:
|
a)
|
b)
|
Kviz rozdělení pohybů.
| křivočarý rovnoměrný | přímočarý nerovnoměrný | otáčivý nerovnoměrný | |
| posuvný | "ještěrka" ve skladu | auto brzdí na dálnici | - |
| otáčivý | ručička hodin | - | kolo motocyklu |
| křivočarý | letadlo - vyhlídka | - | rozběh kolotoče |
| přímočarý - křivočarý | posuvný - otáčivý | rovnoměrný - nerovnoměrný | |
| letadlo model - na plný plyn |
křivočarý | posuvný | rovnoměrný |
| kolo formule závod | křivočarý | otáčivý | nerovnoměrný |
| tok vody v potrubí stálá rychlost |
přímočarý | posuvný | rovnoměrný |
| svisle pustím kámen | přímočarý | posuvný | nerovnoměrný |
| start rakety svisle | přímočarý | posuvný | nerovnoměrný |
nám udává, jakou dráhu urazí těleso za 1 s (1 h).
| dráha s | čas t | rychlost v |
| 5 m | 1 s | 5 m/s |
| 80 km | 1 h | 80 km/h |
| 7 km | 1 s | 7 km/s |
| Rychlost je fyzikální veličina. | |
| Značka: | v (velocity) |
| Základní jednotka: Vedlejší jednotky: |
1 m/s 1 km/h 1 km/s |
Okamžitá rychlost (měříme ji) = rychlost tělesa v
daném okamžiku.
Měří ji:
- tachometr (pro auto,
bicykl)
- radar (pro lib. těleso v pohybu)
- anemometr (pro vítr
-
lopatkové kolo)
- GPS navigace (pro turistu)
-
lano s
uzly (starověká loď)
Tachometr vozidel měří otáčení kola - tím zjistí rychlost.
Živočichům: běžec, želva, gepard, hlemýžď, kůň, dikobraz
přiřaď rychlost: 5 m/h, 60 km/h, 3 km/h, 120 km/h, 36 km/h, 0,5 km/h.
Jak si představit rychlost: 10 m/s, 1 cm/rok, 11 km/s, 150 km/h (vysvětli).
Dobrovolný DÚ: Rychloměr letadla má vně letadla čidlo (není to anténa). Jak čidlo vypadá a jak se jmenuje?
Kviz: skn-okamž×prů
650 - 720 - uplyne 0 h 30 min = 0:30 h
Návod, jak uplynulý čas vypočítat:

| Urči dobu: (ve tvaru 2:15 h) |
630-950= 520-1030= 740-1110= 1030-1440= |
3:20 h 5:10 h 3:30 h 4:10 h |
630-1910= 2330-020= 2210-130= 2150-630= |
12:40
h 0:50 h 3:20 h 8:40 h |
Znát:
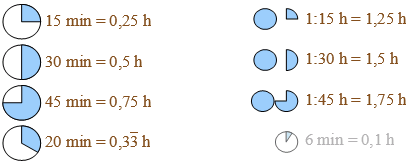
Desetinným číslem: Počet minut:
| 90 min = 75 min = 150 min = 80 min = *12 min = *24 min = |
1,5 h 1,25 h 2,5 h 1,33 h 0,2 h 0,4 h |
1,25 h = 1,33 h = *0,7 h = |
75 min 80 min 42 min |
0,01 h = 1 h/100 = 3600/100 = 36 s
0,02 h = 72 s
Přiřaď rychlosti: 50 m/s, 10 m/s,
220 m/s, 1 m/s, 30 m/s chodec 1 m/s, sprint 10 m/s, auto
30 m/s, pád 50 m/s, let 220 m/s
pohybům: sprinter, dopravní letadlo, auto (dálnice), volný pád, chodec
| 1 m/s | ––> (×3,6) ––> | 3,6 km/h |
| 36 km/h | ––> (:3,6) ––> | 10 m/s |
| děj | m/s | km/h |
| chůze sprint rychlá jízda volný pád formule dopravní letadlo zvuk |
1 10 30 50 90 220 334 |
3,6 36 108 180 320 800 1200 |
POZN: pohyb světadílu 5 cm/rok
raketa 7,2 km/s
1 uzel = 0,514 m/s (10 uzlů = 5 m/s = 18 km/h)
projektil (náboj) ~200-2000 m/s
odkaz
světlo 300 000 km/s …
20 m/s = 72 km/h
30 m/s = 108 km/h
40 m/s = 144 km/h … počítej jako násobky 30 km/h (tedy po 10 m/s)
Dobrovolný úkol: Vytvoř prezentaci o 3 nejrychlejších zvířatech (název, kde žije, rychlost v m/s a km/h, proč ji vyvine) - např: suchozemští savci, ptáci, ryby, rychlé pohyby při lovu (chameleon…) nebo vysokých rychlostech těles kolem nás (obvod CD, součásti strojů…).
| Převeď: | 2 m/s = 3 m/s = 10 m/s = 100 m/s = |
7,2 km/h 10,8 km/h 36 km/h 360 km/h |
3,6 km/h = 36 km/h = 72 km/h = 108 km/h = |
1 m/s 10 m/s 20 m/s 30 m/s |
Zpaměti: Jak rychle by muselo jet auto, aby za 2 h urazilo 160 km?
Vždy vypočtená
Je to stálá rychlost, kterou by
auto jelo během celé
jízdy.
např.: za 2 h ujedu 120 km - průměrná rychlost = 60 km/h
| v = | s ––– t |
v = průměrná rychlost, kterou by těleso urazilo dráhu s za čas t.
POMŮCKA: km/h ~kilometry ZA hodinu ~ vzdálenost
(s) / čas (t)
(velocity, time)
| PŘ: Auto ujelo | 180 km dráha s |
za | 3 hodiny čas t |
- jakou průměrnou rychlostí? |
s = 960 km, t = 12
h, v = ? km/h
v = s/t
v = 960/12
v = 80 km/h
Automobil jel průměrnou rychlostí 80 km/h.
(jako by jel celou cestu 80 km/h, nezastavoval, nezrychloval…)
PŘ: 1,2 km do školy ujdu za 13:20 min. Jakou mám průměrnou
rychlost?
s = 1,2 km, t = 13 min 20 s, v = ? m/s
v = s/t t
= 13:20 = 13×60 + 20 = 800 s
v = 1200/800 s = 1,2 km = 1200 m
v = 1,5 m/s
Do školy jdu průměrnou rychlostí 1,5 m/s, tj. 5,4 km/h.
Jednotky:
* m, s -> m/s
* km, h -> km/h
Rychlost po cestě do školy:
Urči svoji průměrnou rychlost po cestě do školy např. pomocí mapy.cz ->
Trasa.
Použij trasu pěší > rychlá, automatickou trasu posuň
dle potřeby (vytvoří se průjezdní body).
- u trasy z domu do školy zjisti délku s (metry)
- změř (na mobilu, hodinkami…) svoji dobu cesty-> čas t (sekundy)
- spočti průměrnou rychlost (m/s)
Zapiš do formuláře v Google učebně.
ukázka
PŘ: Cyklista ujel za 1:40 min 900 m. Jakou rychlostí jel?
Spočítej zpaměti:
| ujetá dráha | za čas | prům. rychlost | jednotka |
| 8 m | 2 s | 4 | m/s |
| 15 km | 3 h | 5 | km/h |
| 80 m | 4 s | 20 | m/s |
| 90 km | 9 h | 10 | km/h |
| 800 m | 100 s | 8 | m/s |
PŘ: Cyklista ujel za 6 minut 1,8 km. Jakou rychlostí jel?
(lze počítat v m/s i km/h)
PŘ: Jihlava 655 –> Rohozná 725 (18
km). Urči průměrnou rychlost.
PŘ: Auto vyjede v 755 z Prahy, v 1040
dojede do Brna (210 km). Urči průměrnou rychlost Praha-Brno.
PŘ: Auto je v 656 v Jihlavě, v 720 v
Havlíčkově Brodu (24 km). Urči průměrnou rychlost Jihlava-Havlíčkův Brod.
PŘ: Auto ujede 500 m za 0:01 h. Urči jeho rychlost v m/s a km/h.
PŘ: Cyklista ujel 6 km za 0:20 h. Urči jeho rychlost v m/s a km/h.
DÚ: zjisti svoji průměrnou rychlost na cestě domů (např. pomocí mapy.cz, příklad).
Budeš měřit:
1. čas pohybu (autíčka, zvířátka, malého sourozence, míčku…) po krátké dráze (doma -
pár metrů).
2. čas průjezdu (3 auta) od horního sloupu v ulici
k dolnímu:
3. vlastní rychlost - např. na vyznačené dráze
50 m před školou, užiješ i čas běhu na 60 m z tělocviku
Do tabulky pak uveď rychlosti dopravních prostředků (m/s, km/h).
Ukázkové výpočty v tabulce nech beze zněn.
LP vypracuj do dokumentu přiloženého k úkolu v Google učebně.
PŘ: Cestovatel v době 550 - 920 urazil 700 km. Čím cestoval? (Tedy jakou měl průměrnou rychlost?)
Rychlost je dána 2 údaji: velikost, směr. Znázorňujeme ji orientovanou úsečkou (obr).
PŘ: Urči dobu jízdy, délku dráhy a průměrnou rychlost
| km | zastávka | příjezd | odjezd |
| 20 | Havlíčkův Brod | 1000 | 1005 |
| 60 | Čáslav | 1045 |
Úkol: Průměrná rychlost cesty do školy v = 4 m/s - jak žák cestuje? (příklady)
Pomocí vzorce v = s/t naplníme pomocný "trojúhelník":
| s |
| v . t |
| Zakrytím počítané veličiny zbude pravá strana vzorce: | s = v.t t = s/v |
PŘ: Jak daleko dojedeš za 2:30 h rychlostí 120
km/h?
v = 120 km/h, t = 2:30 h, s = ? km
s = v.t
s = 120×2,5 t = 2:30 h = 2,5 h
s = 300 km
Automobil za 2,5 h ujel 300 km.
PŘ: V 2250 vyjede auto z Jihlavy (do Prahy). V
kolik asi bude v Praze? (průměrná rychlost ~90 km/h, Ji-Pha ~135 km)
v = 90 km/h, s = 135 km, t = ? h
t = s/v
t = 135:90
t = 1,5 h 1,5 h = 1:30 h
2250 + 1:30 h = 020 h
Auto bude v Praze asi v 020 h.
PŘ: Za jak dlouho ujede auto 960 km průměrnou rychlostí 80 km/h?
s = 960 km, v = 80 km/h, t = ? h
t = s/v
t = 960/12
t = 12 h
Auto ujede 960 km za 12 hodin
PŘ: Jak daleko uletí letadlo za 3 h rychlostí 100 m/s?
t = 3 h, v = 100 m/s, s = ? km
s = v.t
s = 360 . 3
v = 100 m/s = 360 km/h
s = 1080 km
Letadlo uletí 1080 km.
PŘ: Jak daleko dojede náklaďák od 650 do 920 rychlostí 20 m/s?
650 - 920 uplyne 10 min + 2 h + 20 min = 2 h
30 min = 2,5 h
t = 2,5 h, v = 20 m/s, s = ?
s = v.t
s = 72 . 2,5 v = 20 m/s = 72
km/h
s = 180 km
Náklaďák za daný čas ujede 180 km.
PŘ: Za jak dlouho ujede cyklista 45 km rychlostí 18 km/h?
PŘ: Jak daleko ujede za 10 minut jezdec rychlostí 15 m/s?
PŘ: V kolik hodin dorazí turista do cíle 10 km vzdáleného, když vyrazil v 820? (rychlost ~1 m/s, zaokrouhluj)
Ukázky: bus Ji-JH , vlak Ji-JH , obrázky (vidce, vitis).
PŘ: Urči dobu samotné jízdy, délku dráhy a průměrnou rychlost. (pomůcka: 6 min = 0,1 h)
| km | zastávka | příjezd | odjezd |
| 70 | Čáslav | 715 | 720 |
| 90 | Kolín | 744 | 750 |
| 150 | Mladá Boleslav | 902 |
PŘ: Urči průměrnou rychlost jízdy Lhota->Nová Ves
| km | zastávka | příjezd | odjezd |
| 15 | Lhota | 755 | 801 |
| 24 | Nová Ves | 831 | 835 |
PŘ: Je 14:35 h, vlak jede v 16:05 h ze stanice vzdálené 6 km.
Stihnu dojít na vlak běžnou chůzí?
(Zvol si, co chceš spočítat: a) dobu potřebnou k chůzi, b) dráhu, kterou v tom
čase ujdu, c) rychlost, kterou bych se musel pohybovat. K vypočtené hodnotě se
vyjádři.)
PŘ: Urči průměrnou rychlost Bílá->Květnov za celý pobyt v autobusu (včetně čekání v Prskoletech).
| km | zastávka | příjezd | odjezd |
| 10 | Bílá | 655 | 701 |
| 12 | Prskolety | 705 | 708 |
| 19 | Květnov | 716 | 718 |
PŘ: Urči průměrnou rychlost Ďáskov->Stoklasy samotné jízdy vlaku (bez čekání v Úvozu).
| km | zastávka | příjezd | odjezd |
| 20 | Ďáskov | 801 | 810 |
| 30 | Úvoz | 827 | 832 |
| 38 | Stoklasy | 845 | 848 |
Kviz: Jízd. řád-skn
Osa –––––– je vždy ČAS.
Graf dráhy s-t (~PÁSMO natažené od startu):
- jede pryč / , jede sem
\
- stojí ––
Úkol: do grafu dráha s-t vyznač ujeté vzdálenosti pro
1. - 6.
minutu, když auto jede rychlostí 60 km/h.
Úkol: do grafu dráha s-t vyznač polohu auta, které:
- 1 h jede 50 km pryč
- 1 h stojí
- 1 h jede 100 km pryč
- 1 h stojí
- 1 h jede 50 km zpět
Zjisti celkovou ujetou vzdálenost (*průměrnou rychlost).
řeš
Úkol: do grafu dráha s-t vyznač polohu auta, které
je 200 km daleko a pak:
- 1 h jede 100 km ode mne
- 1 h stojí
- 1 h jede 50 km pryč
- 1 h jede 100 km ke mně
- 1 h jede až ke mně
Zjisti celkovou ujetou vzdálenost (*průměrnou rychlost).
řeš
Úkol: do grafu dráha s-t vyznač polohu auta, které:
- 1 min stojí
- 1 min jede rychlostí 60 km/h
- 1 min jede rychlostí 120 km/h
- 1 min stojí
- 1 min se vrací rychlostí 60 km/h
Úkol: 830 Jihlava (0. km)
930 Brno (100. km)
1030 Brno (100. km)
1230 Ostrava (300. km dálnice)
Nakresli graf s-t, urči ujetou vzdálenost a průměrnou rychlost.
Graf rychlosti v-t (tachometr):
- zrychluje /, zpomaluje
\
- stálá rychlost ––
- stojí-li, je čára –– na ose x!
Úkol: do grafu rychlost v-t vyznač polohu auta, které:
- 1 h jede 100 km/h
- 1 h stojí
- 2 h jede 50 km/h
- 1 h jede 25 km/h
Zjisti celkovou ujetou vzdálenost (*průměrnou rychlost).
řeš
Úkol: do grafu rychlost v-t vyznač polohu auta, které:
- 1 min zrychluje na 60 km/h
- 1 min jede 60 km/h
- 1 min jede 120 km/h
- 1 min jede 60 km/h
- 1 min brzdí až zastaví
Urči ujeté vzdálenosti, celkovou vzdálenost a průměrnou rychlost.řeš
Úkol: do grafu rychlost v-t vyznač polohu auta, které:
- 1 h jede 80 km/h
- 2 h jede 40 km/h
- 2 h stojí
- 1 h jede 80 km/h
Zjisti ujeté vzdálenosti, celkovou ujetou vzdálenost, průměrnou rychlost během
jízdy.řeš
Tachograf (obr)- na papírové kolečko
(nebo čip) zapisuje okamžitou rychlost náklaďáku.
Grafikon - znázornění např.
pohybu vlaků v jediném grafu s-t. (ukázka1,
ukázka2)
Úkol:
Zanes do grafu s-t:
- z Brna vyjel v 900 h
- ve Velkém Meziříčí stál 920-950
- do Prahy dojel v 1110 h
Brno–(50 km)–Velké Meziříčí–(150 km)–Praha.
Spočti průměrnou rychlost samotné jízdy cestou do Prahy.
*Mohl celou cestu jet a dodržovat povolenou rychlost?
Porovnání pohybu míčku na nástupišti a ve vlaku.
Kviz grafy jednotlivě dvojice